Spatial interpolation

Tese de conclusão acadêmica (Projeto 1)

Esta seção conterá o desenvolvimento do último projeto de faculdade realizado na Universidade Estadual de São Paulo (Unesp). O trabalho será centrado na manipulação de dados espaciais e métodos geoestatísticos.

Repositório oficial: Github: spatial-interpolation

Desenvolvimento

Estações pluviométricas: Método IDW e Variograma para as estações pluviométricas na Bacia de Tamanduateí

Stack: ArcPy, Pandas, NumPy, R e ArcGIS

Hipótese: O objetivo primário deste trabalho era comparar as várias combinações de pluviômetros dentro da Bacia de Tamanduateí, dividindo-se em 1/3 dos pluviômetros para teste e 2/3 para treinamento.

A primeira fase do trabalho consistiu em trabalhar com pluviômetros na região de Tamanduateí (TTI) - São Paulo. Foram selecionados cerca de 24 estações pluviométricas para realizar o processo de interpolação com o método de IDW (Inverse Distance Weigh). Para averiguar a interpolação foram selecionados 4 pluviômetros de teste separadas ao longo da área de estudo TTI e cerca de 16 estações escolhidas aleatoriamente para realizar a interpolação.

Código da geração de Raster resultantes da interpolação: Clique aqui

Para demais códigos de randomizar as estações pluviométricas conforme a proporção estabelecida e análise dos resultados: Clique aqui

Os resultados demonstraram grande desvio com relação aos pluviômetros de teste, indicando que interpolação linear não era um método adequado as estações pluviométricas analisadas.

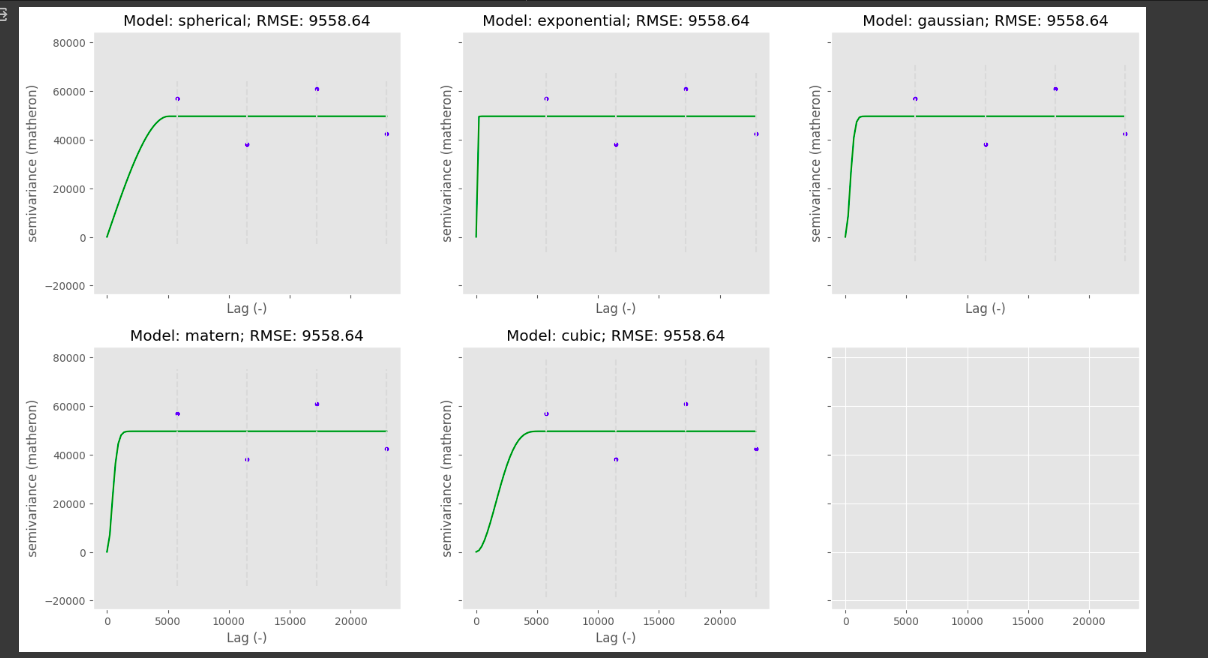
Cálculo do semiovariograma nas estações pluviométricas

Stack: Pandas, Numpy, Pykrige

O semivariograma indica que não há continuidade espacial entre os dados. Conforme a imagem abaixo:

À medida que os lags aumentam a semivariância por vezes aumenta e por vezes diminui indicando que há descontinuidade espacial entre os dados;

Dados de radar

Na segunda etapa da pesquisa, foram utilizados dados de Radar. Estes dados são primariamente extraídos em formato binário (.raw). Vamos aplicar metodologia análoga aos dados de pluviômetro.

Como os dados são captados a cada minuto, temos cerca de 12k arquivos para converter.

A janela temporal selecionada compreende aos primeiro trimestre de 2019.

Processamento dos dados de Radar

Os dados brutos do Radar estão em formato binário além de captar a refletividade. É necessário, portanto, converter a refletividade para precipitação.

Para executar este procedimento, foi utilizado o repositório público da pesquisadora Aurelliene para processar e converter os dados: Repositório Git Hub

Recorte espacial

Primeiramente foi realizado um recorte para região de RMSP. Conforme as coordenadas:

Extensao total do Radar Sao Roque (CAPPI)

1. nx = 500
2. ny = 500
3. dx = 0.009957
4. dy = -0.0090014
5. x1 = -49.5786
6. y1 = -21.3379 + ny*dy

Recorte RMSP + 10km

1. xMin = -47.298125
2. yMin = -24.153483
3. xMax = -45.604801
4. yMax = -23.092909

Por meio de um Bash Script, é orquestrado as funções de recorte espacial e conversão para precipitação (Marshall Palmer):

#!/bin/bash

for filename in $(ls /dados/radar/saoroque/cappi/cappi3km/2020/03/*.raw); do
  python ./recorte_radar.py ${filename} /dados/radar/saoroque/cappi/cappi3km_sp/2020/03/
done

for filename in $(ls /dados/radar/saoroque/cappi/cappi3km_sp/2020/03/*.raw); do
  python ./gera_bin_prec.py ${filename} /dados/radar/saoroque/cappi/cappi3km_sp_prec/2020/03/
done

A matriz de alcance do radar é de 500x500, após o recorte para região de RMSP, resulta-se em uma matriz 120x172.

Conversão dos dados de radar

Através da função ´gera_bin_prec.py´ é realizado a conversão de Marshall-Palmer (refletividade para precipitação).

Repassando as dimensões da matriz oriunda do recorte espacial (120x172) temos:

import os
import sys
import numpy as np

dbz_file = sys.argv[1]
path_out = sys.argv[2]
basename = os.path.basename(dbz_file)

#nx = 666
#ny = 666
#nx = 27
#ny = 29
#Dimensão da matriz gerada em recorte_radar.py
nx = 120
ny = 172
dbz = np.fromfile(dbz_file, dtype=np.float32).reshape(ny, nx)
prec = np.full((ny, nx), -99.0, dtype=np.float32)

for x in range(nx):
    for y in range(ny):
        if dbz[y, x] != -99 and dbz[y, x] <= 36:
            prec[y, x] = ((10**(dbz[y, x]/10))/200)**0.625
        elif dbz[y, x] > 36:
            prec[y, x] = ((10**(dbz[y, x]/10))/300)**0.714

prec_file = os.path.join(path_out, basename)
with open(prec_file, 'wb') as fn:  # Escrita do arquivo como binario
    fn.write(prec)

Junção dos dados processados

Agora que obtivemos todos os dados em termos de precipitação, temos que concatenar os três meses consecutivos.

Para isso, foram somadas todas a matrizes geradas de precipitação.

#função de processa dados de radar
def process_radar_data_monthly(PATH):
    initial_matrix = np.zeros((NX, NY))
    #processar dados binários
    for name_file in os.listdir(PATH):
        with open(os.path.join(PATH, name_file), 'r') as file:
            binary = np.fromfile(file, dtype=np.float32).reshape(NX, NY)
        temp_val = binary
        initial_matrix+=temp_val
    # todas as matrizes de precipitação são somadas à variavel initial_matrix
    return initial_matrix

def plot_radar(radar_matrix):
    #plot radar
    plt.imshow(radar_matrix, cmap = 'Blues')
    plt.colorbar()  

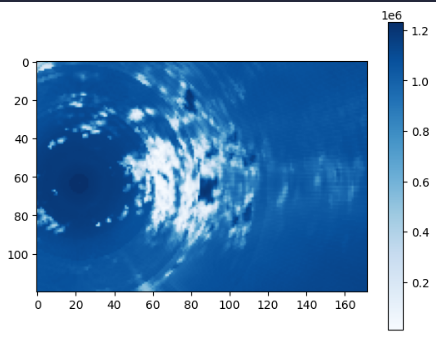
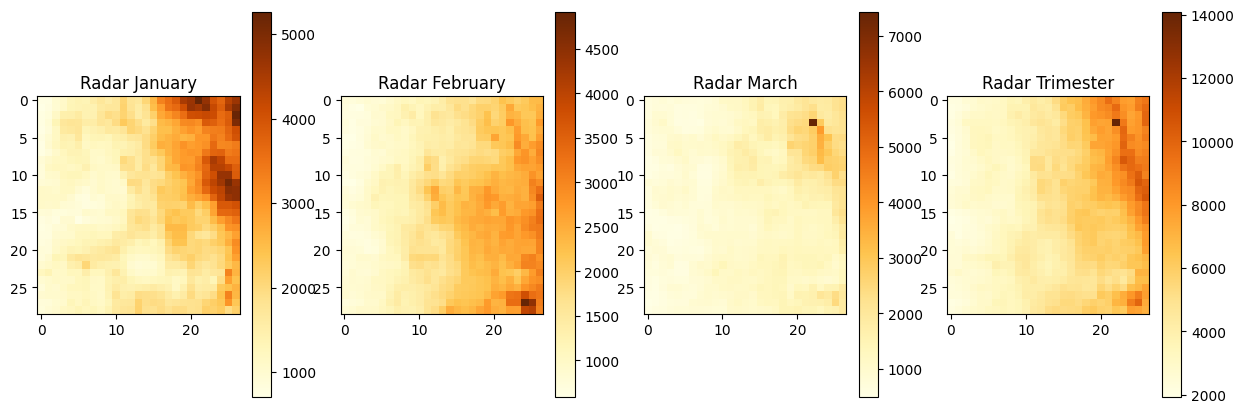
Os valores de conversão estão negativos, portanto, é realizado a operação np.abs(trimester_data). Ao final com a função plot_radar, obtemos:

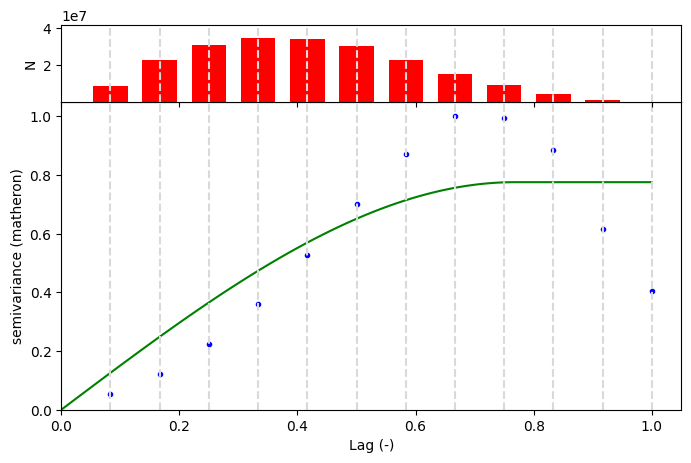
Variograma e Semivariograma

O semivariograma demonstrou um comportamente atípico na qual a variação ocorre de maneira semelhante a uma função trigonométrica (senóide).

Foram ajustados alguns parâmetros que causavam ruído. Desta forma, obteve-se um semivariograma mais condizente á realidade. Não foi possível adicionar mais lags ao algoritmo de cálculo de semivariograma, visto o alto volume de dados, o Kernel para de ser executado.

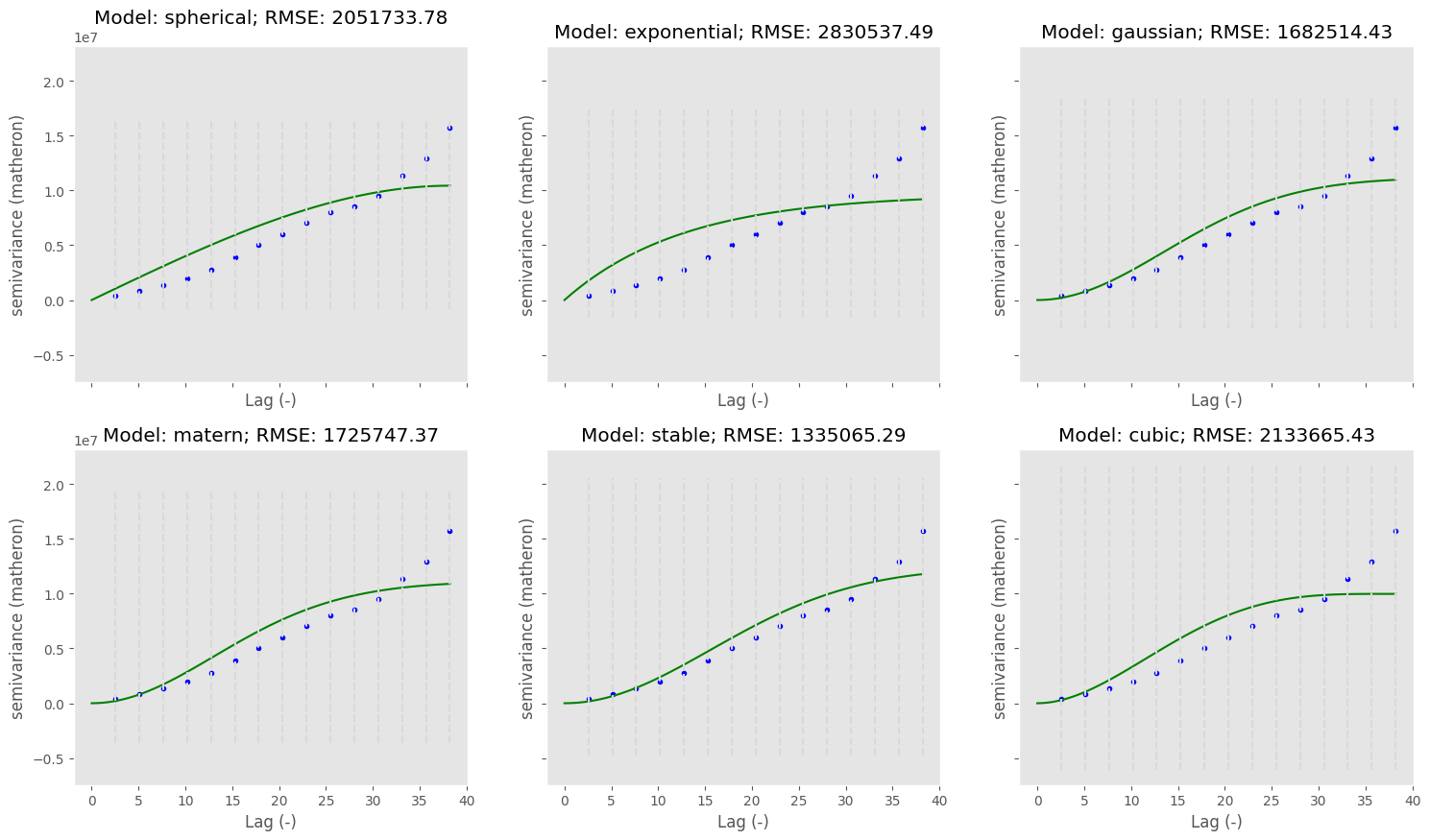
Recorte espacial na região de Tamanduateí (TTI)

Aplicando-se os processos supracitados podemos realizar novamente o recorte espacial.

1. xMin = -46.6608
2. yMin = -23.7568
3. xMax = -46.4041
4. yMax = -23.514

Para Tamanduateí, há continuidade espacial evidente.

Investigação dos valores de precipitação

Ao realizar a conversão Marshall Palmer e realizar a soma trimestral da precipitação obtemos valores de pico próximo entre 5000mm e 7000mm em algumas células. Deve-se analisar se este valor condiz com a realidade.

Lembrando que o procedimento da obtenção do acumulado de precipitação é análogo ao processo usado pela pesquisadora Aurelliene

Em (gera_acum_prec_daily.py) é realizado a seguinte operação obtenção dos valores de precipitação acumulada diária:

dir_input = "/dados/radar/saoroque/ppi/prec_tamanduatei_box/2015/01"
out = open('acum_prec_daily.csv','w')
start = datetime.strptime(sys.argv[1], "%Y%m%d")
end = datetime.strptime(sys.argv[2], "%Y%m%d")

dict = {}
datehour = start
acum = np.full((NX, NY), 0, dtype=np.float32)

while datehour <= end:
    pattern = datetime.strftime(datehour, "*%Y%m%d*")
    files = glob.glob(os.path.join(dir_input, pattern))
    for file in sorted(files):
        prec = np.fromfile(file.strip(), dtype=np.float32).reshape(NX, NY)
        np.place(prec, prec==-99, 0.0)
        np.place(prec, prec<1, 0.0)
        acum = np.add(prec, acum)

    datehour_str = datetime.strftime(datehour, "%Y%m%d")
    dict[datehour_str] = np.sum(acum)
    out.write(datehour_str+","+str(dict[datehour_str])+"\n")
    datehour = datehour + timedelta(days=1)
    acum = np.full((NX, NY), 0, dtype=np.float32)

Os valores -99 e valores menores que 1 do arquivo binário (.raw) são convertidos para 0 . Desta forma a matriz importada prec é somada à matriz anterior. Ilustrando a seguinte equação.

Seja $[M_{i,j}]_n $,

a matriz produto da conversão de Marshall-Palmer, $S_{i,j}$ a matriz final obtida diária e $I_{i,j}$ uma matriz de zeros temos que:

Inicialmente a somatório no código recebe a matriz inicial de zeros: $S_{i,j} = I_{i,j}$, no qual, dentro do laço temos:

$S_{i,j}$ = $\sum^n_1 [M_{i,j}]_n$ (1)

Sendo $n$ o número de arquivos binários convertidos em matrizes que correspondem ao recorte temporal analisado.

Hora, se o valor final da matriz de acumulo diário é a soma de todas as matrizes do período correspondente, logo a soma trimestral ou de qualquer recorte temporal, é a soma sucessiva de matrizes de mesma dimensão que correspondem ao local analisado.

Portanto, analogamente temos:

#função de processa dados de radar
def process_radar_data_monthly(PATH):
    initial_matrix = np.zeros((NY, NX))
    #processar dados binários
    aux = 0
    for name_file in os.listdir(PATH):
        with open(os.path.join(PATH, name_file), 'r') as file:
            binary = np.fromfile(file, dtype=np.float32).reshape(NY, NX)
        temp_val = binary
        np.place(temp_val, temp_val==-99, 0.0)
        np.place(temp_val, temp_val<1, 0.0)
        initial_matrix+=temp_val
        aux+=1
    print(f'Interações:{aux}')
    return initial_matrix

Por fim, obtemos o plot mensais e trimestral.

O que representa 5000m em um mês de acumulado?

Vamos calcular a distância do retângulo permeia a área de estudo. Como a área é um retângulo $x \times h $, sendo $x$ e $h$ a base e a altura respectivamente.

Temos uma extensão de aproximadamente 705km² distribuídos ao longo de 783 pixeis regulares. Logo temos um acúmulo em janeiro de 5000mm distribuídos ao longo de 0,9km². Aproximadamente $0.0056mm/m²$.